\(k\)-shape

Sage does not have a builtin ‘kShape’ object. This module contains useful functions pertaining to \(k\)-shapes:

AUTHORS:

• Matthew Lancellotti (2018): Initial version

REFERENCES:

[genocchi]

(1, 2, 3, 4) Combinatorics of k-shapes and Genocchi numbers, in FPSAC 2011, Reykjav´k, Iceland DMTCS proc. AO, 2011, 493-504.

k_shape.h_bounds(p, k, width)

Recall the \(H_i\) as defined in Definition 3.3 of [genocchi].

Given a natural number k (used for the \(k\)-shape or \(k\)-boundary) and a width width, returns \((y_\text{min}, y_\text{max})\), the two vertical coordinates which define the horizontal strip.

EXAMPLES:

The 4-boundary of partition (10, 7, 4, 2, 2, 2, 1, 1, 1, 1) is shown below on a cartesian plane with the vertical lines corresponding to the vertical bounds shown in blue.

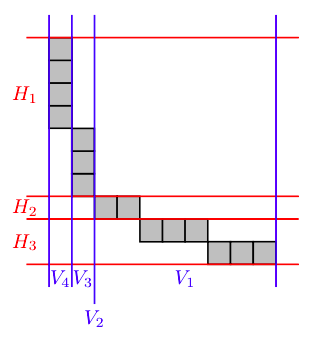
sage: h_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=3)
(0, 2)
sage: h_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=2)
(2, 3)
sage: h_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=1)
(3, 10)

sage: h_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=99)
(0, 0)
sage: h_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=0)
Traceback (most recent call last):
...
ValueError: min() arg is an empty sequence

See also

v_bounds()

k_shape.is_irreducible(s, k)

A k-shape ptn is called irreducible if there does not exist a \(k\)- or \(k-1\)-rectangle corresponding to both the \(k\)-row-shape and \(k\)-column-shape of \(ptn\).

For a more rigorous definition, see Definition 3.7 of [genocchi].

Given a \(k\)-shape ptn and a natural number k, returns True if and only if ptn is irreducible.

(Also, a \(k\)-shape is irreducible if and only if it is not reducible.)

EXAMPLES:

The partition [3, 2, 1] has 3-row-shape [2, 2, 1] and 3-column-shape [2, 2, 1]. It is not 3-irreducible because there exists a 2x2-rectangle R in the 3-row-shape and the cells that make up R when viewed in the 3-column-shape form a 2x2-rectangle (you can’t see it, but the 2’s are switched here):

sage: is_irreducible(Partition([3, 2, 1]), k=3)
False

In this example, no good rectangle can be found, making it irreducible:

sage: is_irreducible(Partition([5, 3, 2, 1, 1]), k=4)
True

See also

is_reducible(), k_to_irreducible_k_shapes()

k_shape.is_k_reducible_by_rectangle(p, k, hw)

Checks if the k-shape is \(k\)-reducible for a \(k\)-rectangle of specific dimensions \(h\) x \(w\).

See Proposition 3.8 in Combinatorics of k-shapes and Genocchi numbers.

INPUTS:

• p – a Partition (and a \(k\)-shape)
• k – the \(k\) of the \(k\)-shape
• hw – an ordered pair hw = \((h, w)\), where \(h\) is the height of the rectangle and \(w\) is the width.

EXAMPLES:

sage: Partition([1]).is_k_reducible_by_rectangle(1, (1,1)) sage: True sage: Partition([2, 1]).is_k_reducible_by_rectangle(1, (1,1)) sage: True sage: Partition([1, 1]).is_k_reducible_by_rectangle(2, (1,1)) sage: False sage: Partition([1, 1]).is_k_reducible_by_rectangle(2, (1,2)) sage: True sage: Partition([1, 1]).is_k_reducible_by_rectangle(2, (2,1)) sage: False

See also

is_reducible()

k_shape.is_k_shape(ptn, k)

A partition is a \(k\)-shape if its \(k\)-boundary has row-shape and col-shape that are partitions themselves. (Definition 2.1 of [genocchi])

Given a Partition ptn and a natural number k, returns True if and only if ptn is a \(k\)-shape.

Given a Partition ptn only, returns True if and only if there exists some \(k \in [1, n-1]\) such that ptn is a \(k\)-shape.

EXAMPLES:

sage: is_k_shape(Partition([3, 1]), 1)
False
sage: is_k_shape(Partition([3, 1]), 2)
True

k_shape.is_reducible(ptn, k)

A k-shape ptn is called reducible if there exists a \(k\)- or \(k-1\)-rectangle corresponding to both the \(k\)-row-shape and \(k\)-column-shape of \(ptn\).

For a more rigorous definition, see Definition 3.7 of [genocchi].

Note that this is different than the definition of a reducible partition!

Given a \(k\)-shape ptn and a natural number k, returns True if and only if ptn is reducible.

(Also, a \(k\)-shape is reducible if and only if it is not irreducible.)

EXAMPLES:

The partition [3, 2, 1] has 3-row-shape [2, 2, 1] and 3-column-shape [2, 2, 1]. It is 3-reducible because there exists a 2x2-rectangle R in the 3-row-shape and the cells that make up R when viewed in the 3-column-shape form a 2x2-rectangle (you can’t see it, but the 2’s are switched here):

sage: is_reducible(Partition([3, 2, 1]), k=3)
True

In this example, no good rectangle can be found:

sage: is_reducible(Partition([5, 3, 2, 1, 1]), k=4)
False

See also

is_irreducible(), k_to_irreducible_k_shapes()

k_shape.k_to_irreducible_k_shapes(k)

Given a natural number k, return a list of all irreducible \(k\)-shapes.

Note that the algorithm runs very slowly after \(k=4\) :(.

EXAMPLES:

sage: k_to_irreducible_k_shapes(3)
[[], [1], [2, 1]]

See also

is_reducible(), is_irreducible()

k_shape.v_bounds(p, k, height)

This is \(V_i\), the vertical analog of h_bounds().

EXAMPLES:

The 4-boundary of partition (10, 7, 4, 2, 2, 2, 1, 1, 1, 1) is shown below on a cartesian plane with the vertical lines corresponding to the vertical bounds shown in blue.

sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=4)
(0, 1)
sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=3)
(1, 2)
sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=2)
(2, 2)
sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=1)
(2, 10)

sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=99)
(0, 0)
sage: v_bounds(Partition([10, 7, 4, 2, 2, 2, 1, 1, 1, 1]), k=4, width=0)
Traceback (most recent call last):
...
ValueError: min() arg is an empty sequence

See also

h_bounds()